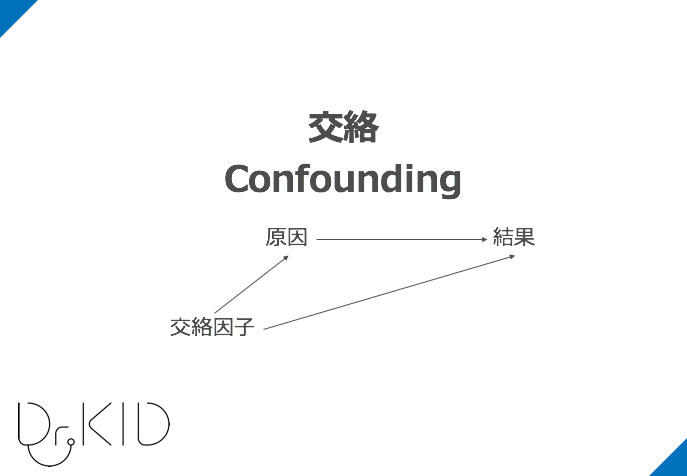
- 『交絡因子ってなんですか?交絡ってなんですか?』
- 『観察研究では、そのまま治療群と非治療群を解析してはいけないのですか?』
- 『交絡ってバイアスですか?』
- 『シンプソンのパラドックス(Simpson’s Paradox)って何ですか?』
などなど、交絡(Confounding)や交絡因子(Confounder)に関する質問を受けることが多数あります。
実は分かっているようで、分かっていない交絡因子。
今回は実例をみながら、交絡や交絡因子に関する理解を深めていけたらと思います。
交絡の実例
いきなりですが、以下の例をご自身に当てはめて考えてみましょう。
あなたは、とある疾患Aの罹ったとします。治療法はなく、1年生存率はおよそ80%です。
ここで新薬Xが発売されました。最近の研究結果から、
- 治療ありの生存率:78%
- 治療なしの生存率:83%
でした。詳しい結果は以下のテーブルになります。
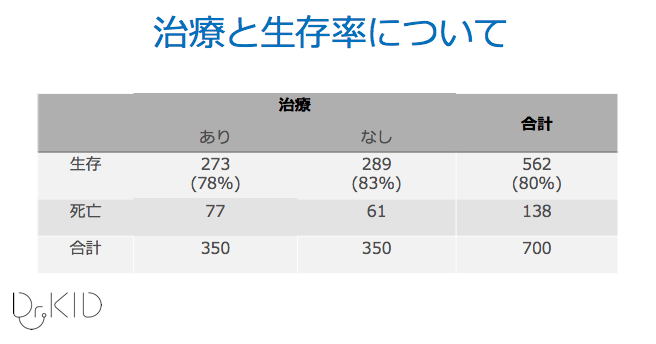
あなたは新薬Xによる治療を受けますか?
データの背景を知ることも重要
上のデータだけをみると生存率の高い方を選ぶのが自然でしょう。
つまり、ほとんどの方が「新薬Xによる治療を受けない(生存率83%)」を選ぶ方が多いのではないでしょうか?
一方、データーの背景を知っている私は、見かけ上のデータが悪い「治療を受ける(生存率78%)」を選択します。
ちょっと意地悪な質問でしたが、治療をするか、しないかの二者択一を選ぶ際に、どのような背景でデータか知ることが重要です。
それをなしに、数字だけで決断してしまうと、思わぬ落とし穴に入ってしまうことがあります。
データの背景と一言でいっても、
- 研究デザイン:ランダム化比較研究か観察研究か
- 対象患者:年齢、性別、人種、基礎疾患があるか
- 研究場所:国や地域、年代
などが挙げられます。
男女別のデータを見てみましょう
では、次に男女別のデータを見てみましょう。
こちらのデータは、先ほどのテーブルを男女で分けたものになります。
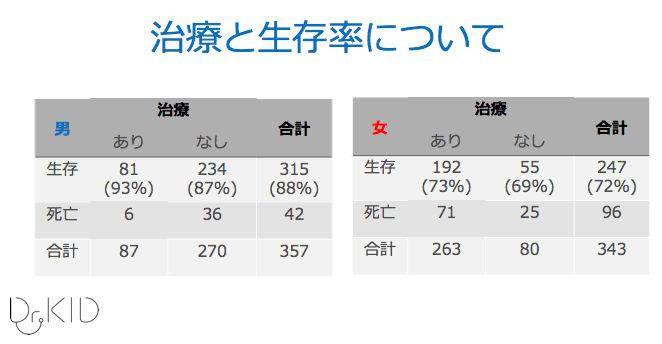
この表によると、
- 治療ありの生存率:男 93% 女73%
- 治療なしの生存率:男 87% 女69%
でした。
ここで、もう一度同じ質問をします。
あなたは治療を受けますか?
(ほとんどの方が、成績の良い治療を受ける、を選ぶことと思います)
交絡と交絡因子
少し混乱されている方がいるかもしれません。なぜなら、男女別に分けない時の治療成績は
- 治療ありの生存率:78%
- 治療なしの生存率:83%
と、「治療なし」ほうが生存率が5%高かったのです。
一方で、男女別に分けた場合は、
- 治療ありの生存率:男 93% 女73%
- 治療なしの生存率:男 87% 女69%
と、男女ともに「治療あり」のほうが生存率が4〜6%ほど高くでています。
「どちらを信じるべきでしょうか?」と質問されてしまいそうですが、基本的には後者のデータ(男女別に分けたもの)でしょう。なぜなら、最初の全体のデータは「交絡」が混入しているからです。
交絡因子とは?交絡とは?
ここからは交絡(こうらく)や交絡因子について説明していきます。
今回でいえば、「性別」が交絡因子といえます。
「古典的な」交絡因子の定義ですが、以下の3つで定義されます:
- 交絡因子(性別)は治療(新薬A)と相関がある
- 交絡因子(性別)は、治療(新薬A)とは関係なしに、アウトカム(生存)と相関がある
- 交絡因子(性別)は治療(新薬A)にもアウトカム(生存)にも影響されない
(つまり、前後関係でいえば、前である)
(*あえて「古典的」といったのは、例外が沢山あるためです。こちらの3つを満たしても必ずしも交絡因子とは限りませんが、ある程度の指標になるのと、基本的な概念を理解するのに役立ちます)
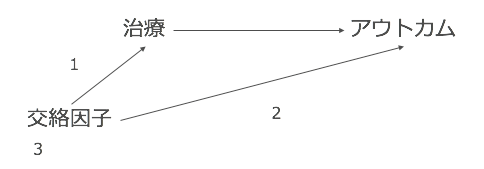
交絡を平たく説明すると、治療とアウトカムの関連を示すデータに交絡因子が入り込んでしまっている状態をいいます。
データから交絡因子を確認する
『どうすればデータから交絡因子を確認できますか?』
と質問されそうですが、上の1〜3を順番に見ていけばよいでしょう。
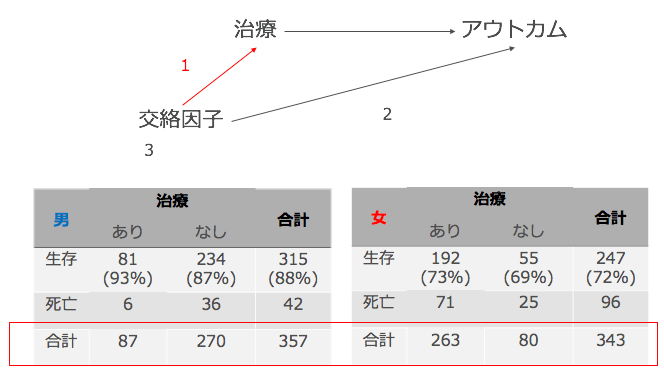
まず1番の矢印(性別 →治療)についてみていきましょう。データは赤で囲った部分が該当します。簡単に説明すると、「性別によって治療をうける割合が異なるか?」を確認すればよいのです。
- 男性における治療ありの割合:24.4%(87/357)
- 女性における治療ありの割合:76.7%(263/343)
となっています。明らかに女性のほうが治療を受ける割合が高くなっています。つまり、1番の矢印(性別 →治療)が成立しているといえます。
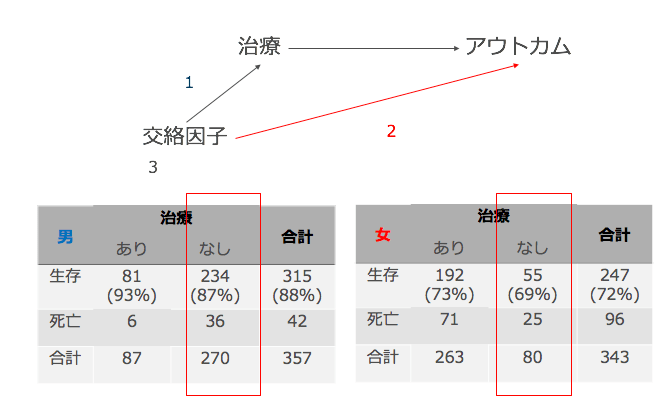
2番の矢印(性別→生存)を見てみましょう。端的に説明しますと「治療を受けない場合、男と女で生存率は異なるか?」を確認すればよいのです。(「治療を受けない」と限定したのは、矢印は「治療」を介していないからです。)
治療を受けない場合の生存率は:
- 男性の生存率:87%(234/279)
- 女性の生存率:69%(55/80)
と、男性のほうが生存率が約20%ほど高かったのです。
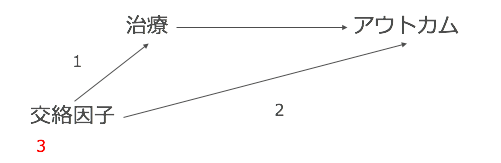
3番の「交絡因子は治療にもアウトカムにも影響されない」については、データで確認するというより、データの背景を考えることが重要です。言われてみると当たり前ですが、
- 性別は治療より前に起こっている
- 性別はアウトカム(治療1年後の生存/死亡)より前に起こっている
といえます。性別は染色体の組み合わせで決定されるので、ここは明らかですよね。
このように1〜3の3つのポイントを意識することで、交絡因子か否かある程度の指標になります。
交絡のあるデータの解釈の仕方
交絡因子について理解が深まったところで、交絡のあるデータの解釈方法について説明していきましょう。
最初の例に戻って見ましょう。最初のデータは、
- 治療ありの生存率:78%
- 治療なしの生存率:83%
という結果で、治療をしないほうが「あたかも」結果がよいように示されています。
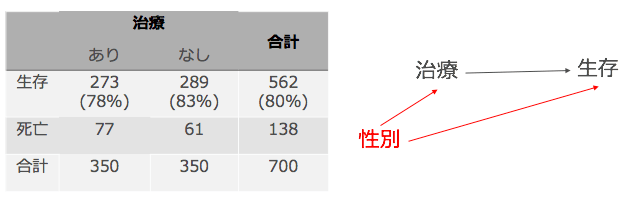
しかし、実際のところ、このデータは2つの経路がごちゃまぜになった結果です。わかりやすくいうと、
- 治療→生存
- 治療←性別→生存
の2つです。ですが、私たちが知りたいのは、前者の(治療→生存)のみです。
層別化によって交絡因子を対処する
では、「治療→生存」の矢印のみを見るにはどうしたら良いでしょうか?
簡単にいえば、赤の経路(治療←性別→生存)を閉じてしまえば良いのです。
「どうやって閉じるのか?」と疑問に思われるかもしれませんが、すでに行ってきました。
男女別に分けて見てしまえばよいのです。このことを「層別化(stratification)」といいます。
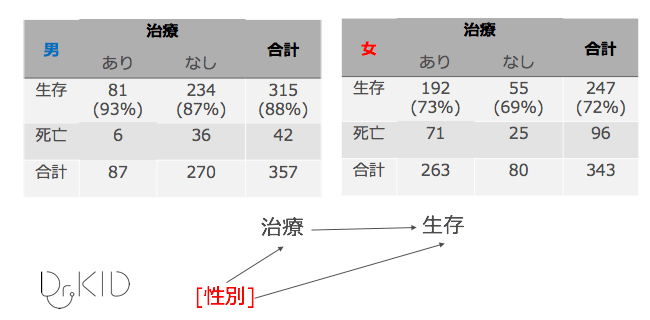
男女を別々に見てしまえば、交絡因子の影響は除去されます。
バイアスについて
次に「バイアス」について説明していきましょう。
その前に、今回の例をRisk Ratio (リスク比) に変換して考えてみましょう。いきなりRisk Ratioと言われても、驚く必要はありません。ただの比ですから。
全体のRisk Ratio、男女別のRisk Ratioは、以下のように計算できます:
- 全体:RR = 0.95 (78% / 83%)
- 男性:RR = 1.07 (93% / 87%)
- 女性:RR = 1.06 (73% / 69%)
となります。
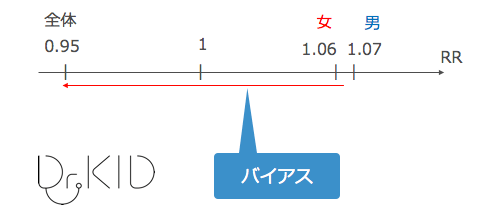
上の図のように、全体の結果は男女別の結果を大きく隔たりがありました。この隔たりのことを「バイアス」と呼びます。
今回でいうと、性別という交絡因子により、交絡によるバイアスが混入したと考えます。
全体の結果を伝えるにはどうしたらよいか?
「男女別のほうが良いとわかりましたが、集団全体の結果を伝えるにはどうしたらよいですか?」と疑問が湧いてくると思います。
これには多数方法があり、
- Mantel-Haenszelの重み付けを使う
- 回帰分析を使う
- そのほかの手法(IP weightingやstandardizationなど)を使う
などの選択肢があります。
例えばMantel-Haenszelの重み付けの数式を使うと、
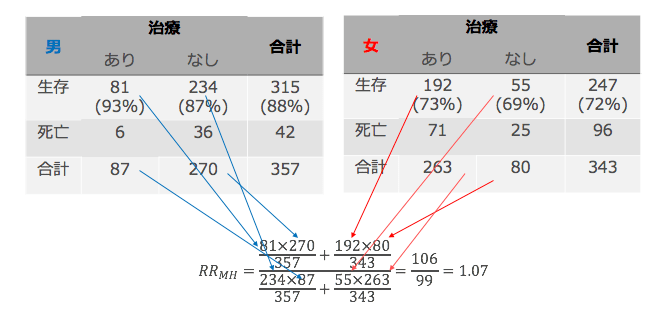
となり、RRMH = 1.07となります。これは男女による違いを統計学的に対処した後の、全体のRRとなります。
以上をまとめると
- 全体:RR = 0.96(性別によるバイアスあり)
- 全体:RRMH = 1.07 (性別によるバイアスなし )
- 男性:RR = 1.07 (性別によるバイアスなし )
- 女性:RR = 1.06 (性別によるバイアスなし )
となります。
まとめ
今回は交絡と交絡因子について、実例から説明してきました。
データをそのまま鵜呑みにしてしまうと、実はバイアスが混入していたというケースも多々あります。
特に観察研究では基本的に交絡因子によるバイアスは混入しているものですので、最初から「バイアスはあるもの」と考え、正しく対処し解釈する必要があります。
●今回の記事は、私が最も尊敬する科学者の1人であるJudea Pearl氏の書籍(Causal Inference In statistics: p2-4)に掲載されているデータを用いて、私のストーリーを組み入れて説明させていただきました。
あわせて読みたい
もう少し交絡因子、交絡、シンプソのパラドックスについて骨太に知りたい方は、KRSK先生のブログをお勧めします。