前回まで、メタ解析の考え方、手法などを8回に分けて説明してきました。

今回は、こちらの論文を用いて、メタ解析を実際に行えればと思います。
Stataでメタ解析を行う際によく使用するコマンド
Stataにはメタ解析を行うコマンドがあり、グラフも自動で作成してくれるため、かなり便利です。
- metan
- metareg
- metacum
- metabias
といったコマンドを使用することがほとんどでしょう。
データを取り込む
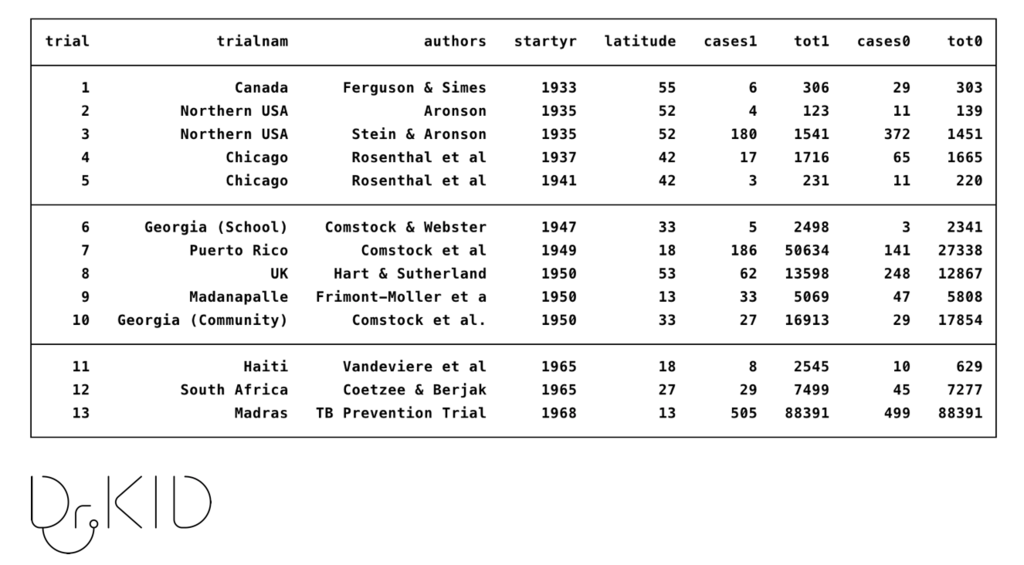
まずはデータをコンピューターに取り込みましょう。
研究によって欲しい情報は異なりますが、今回は
- 研究が行われた場所(trialnum)
- 著者名(authors)
- 年(startyr)
- 緯度(latitude)
- 治療群でアウトカムを発症した人数(cases1)
- 治療群の人数(tot1)
- 非治療群でアウトカムを発症した人数(cases0)
- 非治療群の人数(tot0)
となっています
メタ解析の方法について
かなり大まかにいうと、メタ解析を行う際に決め事が2つあり、
- 固定効果にする or ランダム効果にする
- 個々の研究の重み付けを選ぶ
(Mantel-Haenzel (MH) の重み付け法、Inverse-Variance法など)
になります。
今回は、同じデータ(BCGワクチンの結核予防効果)を使って、4通りの解析をしてみましょう:
- 固定効果 + MH法
- ランダム効果 + MH法
- 固定効果 + Inverse-Variance法
- ランダム効果 + Inverse-Variance法
の4つです。
固定効果 + MH法
こちらが固定効果とMantel-Haenszel法による重み付けをした解析です:
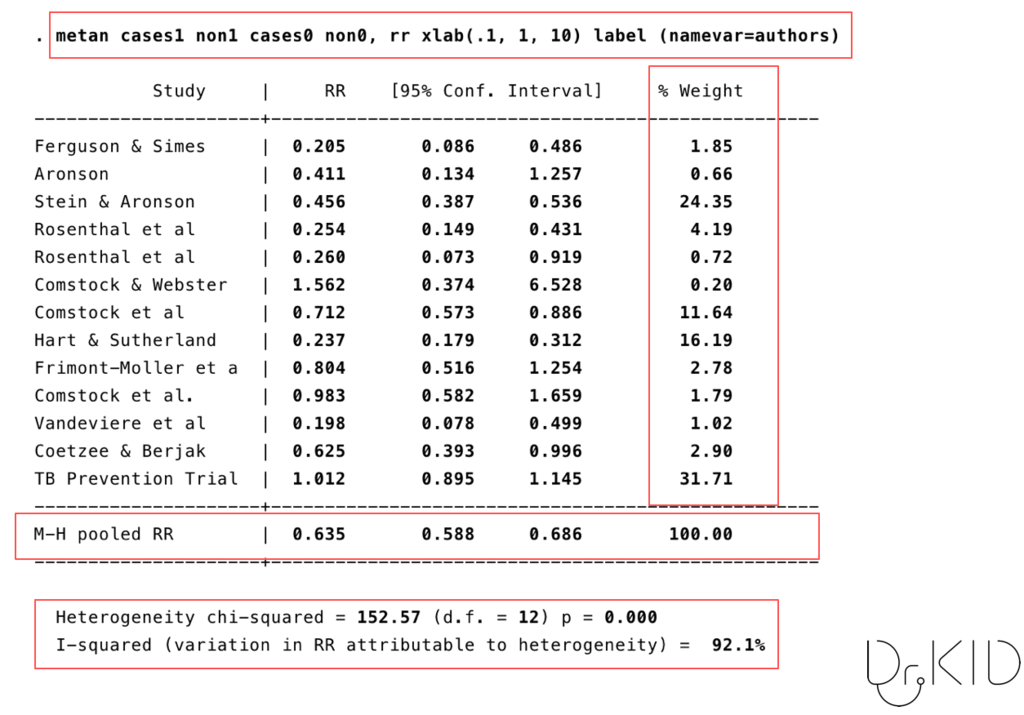
赤で記したところが、主に確認をするところです。
上から順に、
- Stataのコマンド(プログラム)
- 個々の研究の重み付け(%weight)
- 研究を統合した結果:pooled RR = 0.635 (95%CI, 0.588〜0.686)
- 異質性の検定 (P < 0.001), I-squared = 92.1%
となっています。
異質性(Heterogeneity)が非常に高いのがわかると思います。
ランダム効果 + MH法
次は、MH法による重み付けのまま、ランダム効果を試してみましょう。
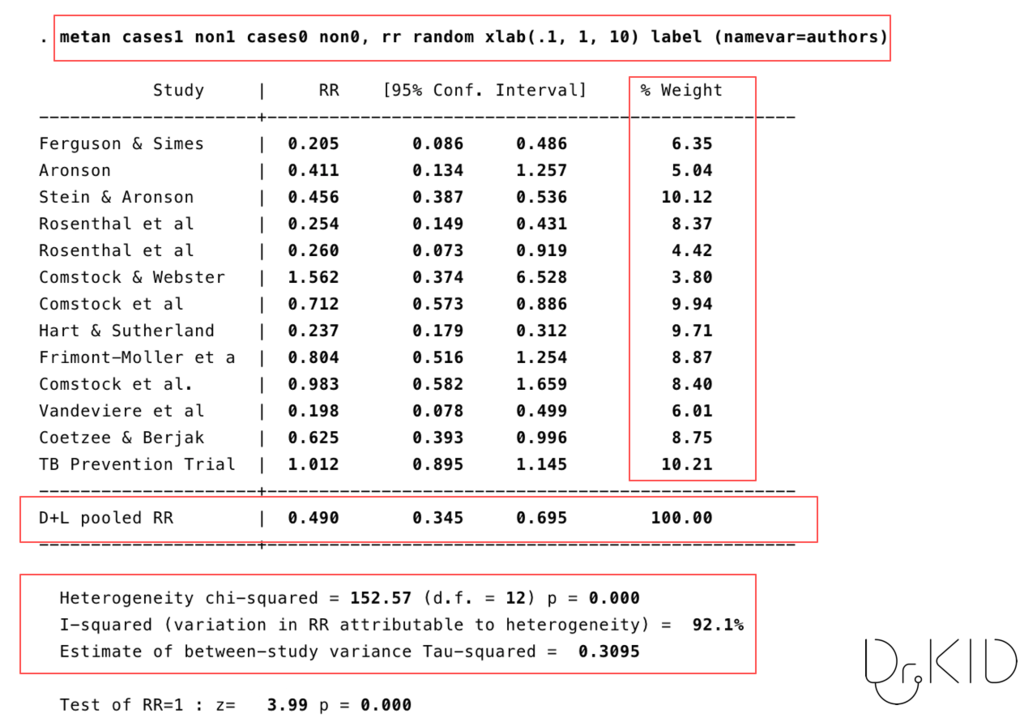
お気づきの方がいるかもしれませんが、最初のmetanから始めるコマンドに”random”を入れただけです。
- 研究を統合した結果:pooled RR = 0.490 (95%CI, 0.345〜0.695)
となっています。
固定効果 + Inverse Variance法
次に、固定効果とInverse Variance法による重み付けをしてみましょう。
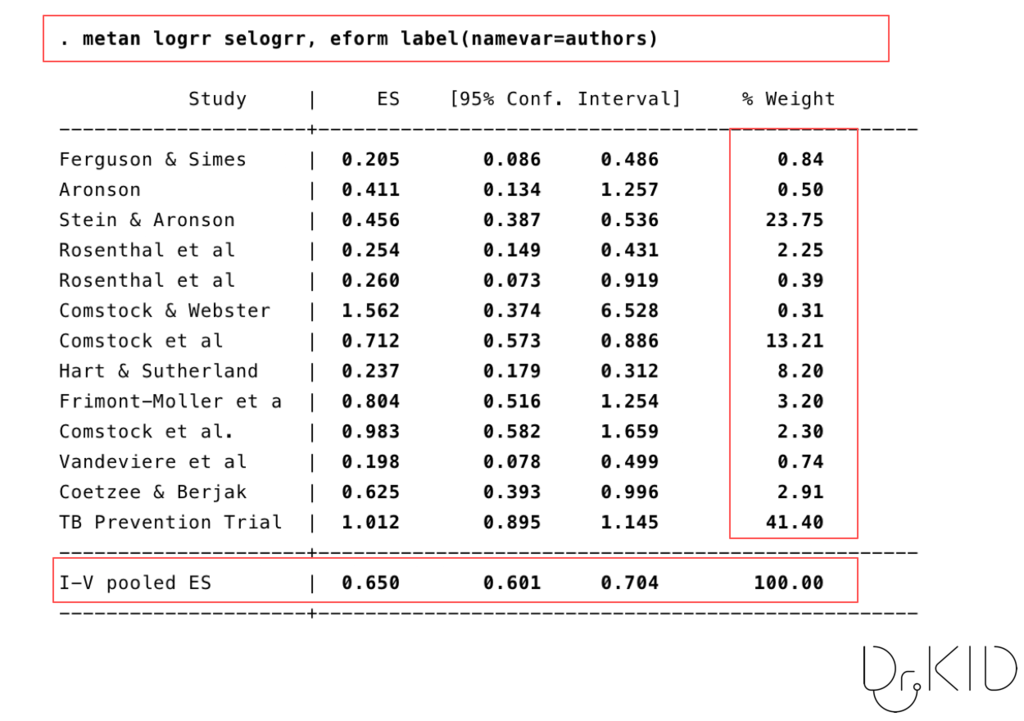
こちらの固定効果 + IV法の結果では、
- 研究を統合した結果:pooled RR = 0.650 (95%CI, 0.601〜0.704)
となっています。
一番最初の結果と少し似通っているのがわかると思います。
ランダム効果 + IV法
最後に、ランダム効果とIV法を使ってみましょう。
metanから始まるコマンドに、randomが追加されています。
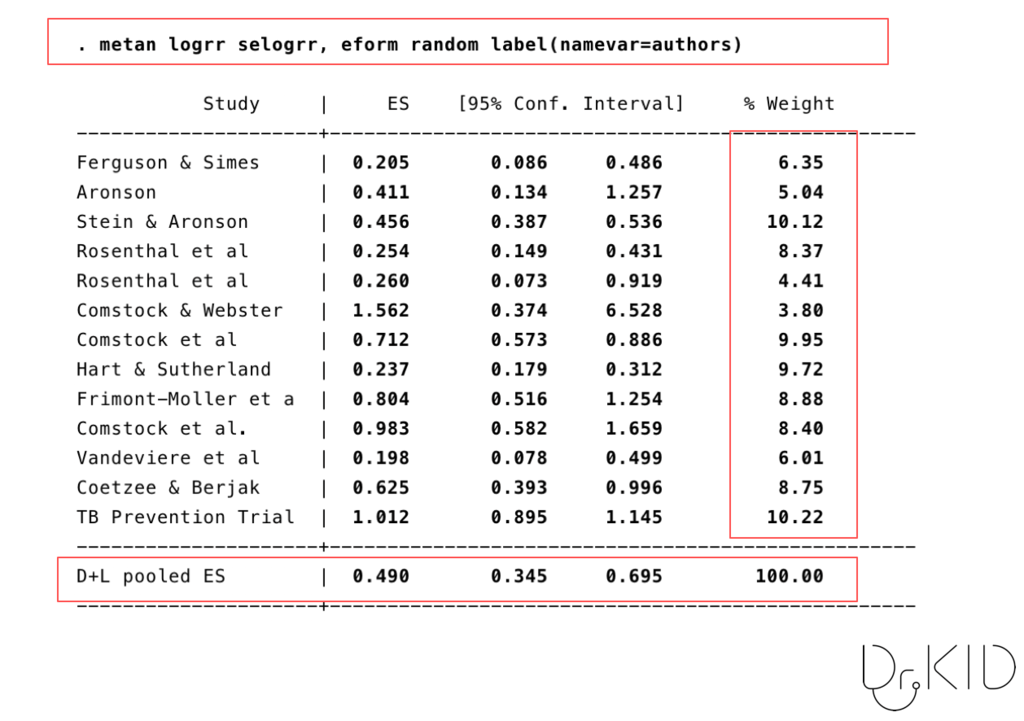
2つめの結果と似通っており、
- 研究を統合した結果:pooled RR = 0.490 (95%CI, 0.345〜0.695)
となっています。
使用した手法によって、結果は異なることもあります
例えば、今回の研究ですと、固定効果 = FE、ランダム効果 = REとすると、
- FE & MH法:RR = 0.635 (95%CI, 0.588〜0.686)
- FE & IV法 :RR = 0.65 (95%CI, 0.601〜0.704)
- RE & MH法:RR = 0.49 (95%CI, 0.345〜0.695)
- RE&IV法 :RR = 0.49 (95%CI, 0.345〜0.695)
となりました。
今回のケースでいうと、MH法を使っても、IV法を使っても、それほどRRは変わらないですし、95%CIの値も近いです。
一方で、ランダム効果(RE)を使用した方が、RRは1から遠ざかり(つまりより予防効果が強い方向へ動き、95%CIも広くなっています。
この現象について説明しようと思います。
1. RR (Risk Ratio)が固定効果とランダム効果で異なる理由
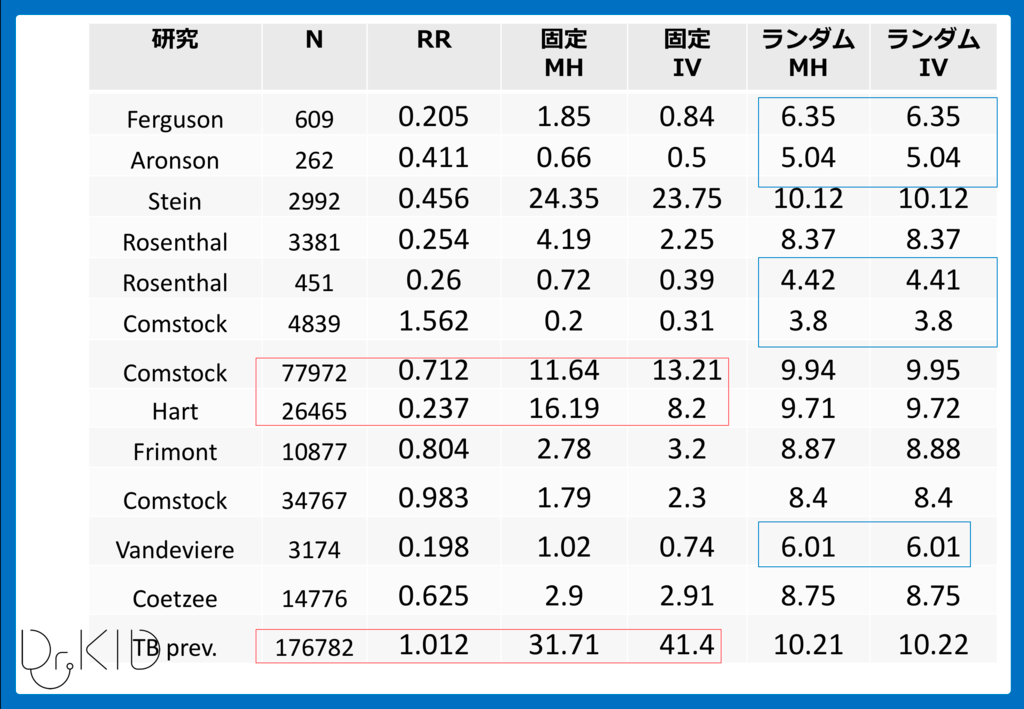
こちらの図は、それぞれ4つの手法で使用した重み付け(%Weight)を並べたものです。
赤で囲ったものが、今回の固定効果の特徴として出ているのですが、
- サンプル数の大きい研究に、より重みをつけている(%Weightが高い)
傾向にあるのがわかります。
特に、最後の「TB prev.」の研究に全体の30〜40%程度の重みがつけられているため、RR = 1.0のほうに研究結果が動きやすくなります。
一方、青で囲ったものが、今回のランダム効果の特徴です。
特徴として
- 固定効果で小さな重みであったが、ランダム効果で重みが増した
研究をつけています。ランダム効果を使った場合、固定効果ほどサンプル数の多い研究に重みをつけすぎず、小さな研究に重みが配分されることが多いです。
このため、固定効果とランダム効果で結果が大きく変動しました。
2. 信頼区間がランダム効果の方が大きい理由
信頼区間の計算をするうえで、分散(ばらつき、variance )を計算するのですが、
- 固定効果:研究内の分散
- ランダム効果:研究内の分散+研究間の分散
から成立しています。
必ずランダム効果のほうが信頼区間が大きくなるとは限りませんが、ランダム効果のほうが分散が大きくなり、信頼区間が広がる傾向にあります。
この研究の問題点
お気づきの方がいるかもしれませんが、この研究では
- 異質性の検定が有意 (P < 0.001)
- I-squared = 92.1%
となっています。
異質性(Heterogeneity)が非常に高く、異質性の原因となる別の因子を考慮したほうがよいことが示唆されます。
次回は、この異質性の対処法について解説していこうと思います。
まとめ
今回は、Stataを使って実際にメタ解析をしてみました。
固定効果とランダム効果、Mantel-Haenszel法とInverse-Variance法を使用して、実例を解説しました。
次回は、異質性の対処を実際にしてみましょう。

おすすめ本はこちら
メタ解析の記事を最初から読みたい