前回、出版バイアスとFunnel Plotの解釈の仕方を説明してきました。
出版バイアス(Publication Bias)がある場合、そもそもメタ解析の結果にバイアスが混入している可能性があることを意味します。
今回は、出版バイアスの統計学的な評価である、
- Begg’s test(Begg検定)
- Egger’s test(Egger検定)
について、さらに
- Trim and Fill method
を簡単に解説していければと思います。
Begg’s test (Begg検定) について
Begg’s testでは、
- (標準化した後の)治療効果
- 治療効果の分散
の順位相関(rank correlation)をみています。
“Rank correlation “というくらいですので、non-parametric検定になります。
(*一方、Egger’s testは parametric検定です)
順位相関(rank correlation)について
Kendall’s tau(τ: ケンドールの順位相関)という指標を使って、この相関をみています。
Kendall’s tau(τ)の数式なところは、統計や疫学を生業にしていないなら理解する必要はありませんが、以下のように計算されています。
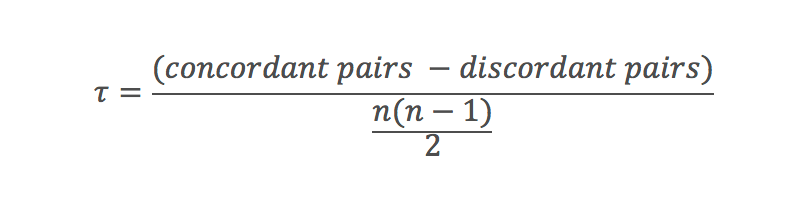
Begg’s testの意味について
この検定では「治療効果(例えばOR)と分散」の相関をみています。
有意差が出た研究も、そうでない研究も、サンプルサイズの大きい研究も、小さい研究も、全てフェアに出版されていたら、相関は0になります。
逆に、分散が小さく(サンプルサイズが大きく)、治療効果の大きな研究ばかりアクセプトされていたら、相関は0から遠ざかります。
このように、治療効果と分散(主にサンプル数)の相関という視点から、出版にバイアスがかかっていないのかを評価しています。
Begg’s testの欠点について
Begg’s test の欠点は、”Non-parametric検定”である点です。
検定力(Statistical power)が弱いので、偽陰性が多いです。
別の言葉でいうと、本当は出版バイアスがあるのに、統計学検定では「出版バイアスなし」と判断してしまうのです。
Egger’s test(Egger検定)について
Egger’s testは
- (標準化した後の)治療効果
- 標準偏差の逆数
を回帰分析の傾き(slope)で検定しています。
Egger’s testの意味について
考え方はBegg’s testと一緒です。
バイアスなく研究結果がアクセプトされていたら、治療効果と標準偏差(の逆数)は無関係であるはずです。
その一方で、例えば、標準偏差の大きい研究が、治療効果が大きい傾向があると解析結果は有意差がでます。
Egger’s testの欠点
Begg’s testと異なり、Egger’s testは parametric検定です。
このため、Egger’s testは偽陰性は少ないのですが、偽陽性が多くなる可能性があります。
特に、Odds Ratioを使用した場合に(標準偏差の計算上)、偽陽性が出やすいといわれています。
出版バイアスを補正する
「じゃあ出版バイアスがあったとして、補正する方法はないのですか?」
と疑問をもたれたかもしれません。賛否両論ありますが、
- Trim and Fill method
という方法で、バイアスを補正することもできます。
Trim and Fill Method について
Trim は整える、Fill は埋めるという意味があります。
その名の通り、Funnel Plotをみて、整えて埋める方法のことをいいます。具体的には
- Funnel Plot を描き
- 出版されなかったであろう研究を足し
- 真の治療効果(effect estimate)を予測する
という方法です。
(*注:あくまでこの研究をTrim & Fill の題材にしているだけですので、研究の妥当性については無視してください)
Trim and Fill の例
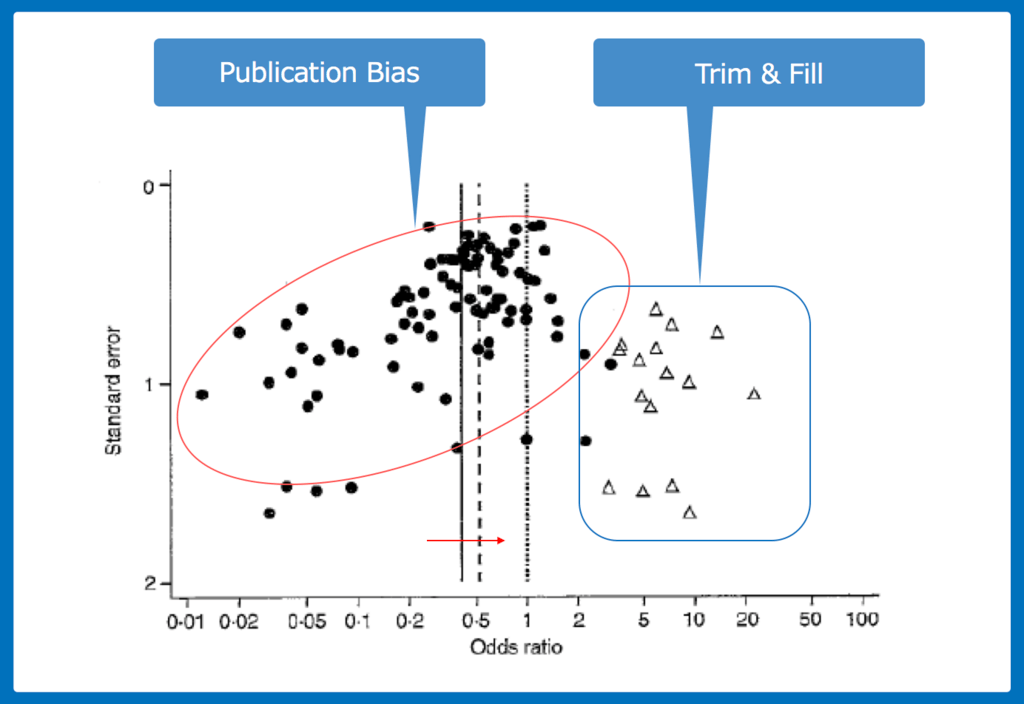
黒丸は論文や学会発表された結果です。
Funnel Plotをしても、明らかに非対称性があり、出版バイアス(Publication Bias)がかかっているのがわかります。
ここで、Funnel Plotがより対称性に近づくように、Plot(三角形)を追加します。
すると、見かけ上は対称性になり、publication biasはある程度は補正できたと考えます(赤矢印)。
現に、
- Publication biasを無視した時は、OR = 0.41(0.34, 0.49)
- Publication biasを補正した時は、OR = 0.56(0.32, 0.97)
と、バイアスが補正されています。
Trim and Fill Method の欠点
この手法はかなり批判の多い手法です。
というのも、
- Funnel Plotで対称性になる
という前提が、そもそも妥当でないかもしれないためです。
また、Funnel Plotを見て非対称性であった場合、必ずしもpublication biasでないこともあります。
「Funnel Plot で非対称 = Publication bias」と考えるのは、あまりに短絡的です。
非対称性の原因となる他の因子も一緒に検討する必要があります。
まとめ
今回はPublication biasの統計学的な評価方法である、Begg’s testとEgger’s testについて解説してきました。
批判も多い手法ですが、Trim and Fill Methodについて、知っておいて損はないでしょう。
次回は、Dose–Response Meta-analysisについて解説していきたいと思います。

おすすめ本はこちら