前回、システマティック(系統的)レビューとメタ解析における、統計学的手法(固定効果とランダム効果)について説明してきました。
固定効果は前提が強すぎるため、ランダム効果のほうが望ましいケースが多いです。ですが、ランダム効果も万能ではないため、その欠点を把握しておくことは非常に重要です。
固定効果とランダム効果について理解すると、すぐに使用したくなりますが、その前に出版バイアス(Publication Bias)について理解をしておいたほうが良いです。
出版バイアス(Publication Bias)がある場合、そもそもメタ解析の結果にバイアスが混入していることを意味します。
出版バイアス(Publication bias)について
『お蔵入り問題(File-drawer problem)』を知ってますか?
多くの医学雑誌は『統計学的有意差のある研究』をアクセプトして出版しています。
『統計学的な有意差』が研究で証明されたからといって、真に治療効果があるかどうかわかりません。
なぜなら、
- 偶然に(by chance)有意差が出た
- 交絡因子が十分に対処されていない
- 選択バイアスがある
- 誤分類がある
といった可能性があるわけです。
P値の功罪について
P値を用いることで、数字として差をみれるわけですが、欠点もあります。
真に治療効果がなかったとしても、P値(P-value)を0.05でカットオフしてしまうと、
- 5%の『Type I error (偽陽性)の研究』が出版され
- 95%の『有意差の出なかった研究(本当は正しい結果)』は出版されない
という現象が起こります。
つまり、真実はお蔵入り(File-drawer)してしまうわけです。
このことを『お蔵入り問題(File-drawer problem)』と名付けられています(by Rosenthal (1979))

このお蔵入り問題と出版バイアスは密接にリンクしていますが、出版に影響する因子として、
- P値
- サンプル数
が出版に大きな影響を与えています。
P値が低い方が、研究参加者数(サンプル数)が多いほうが、出版されやすい傾向にあります。
P値のハッキング(P-value hacking)は実際に起こっている
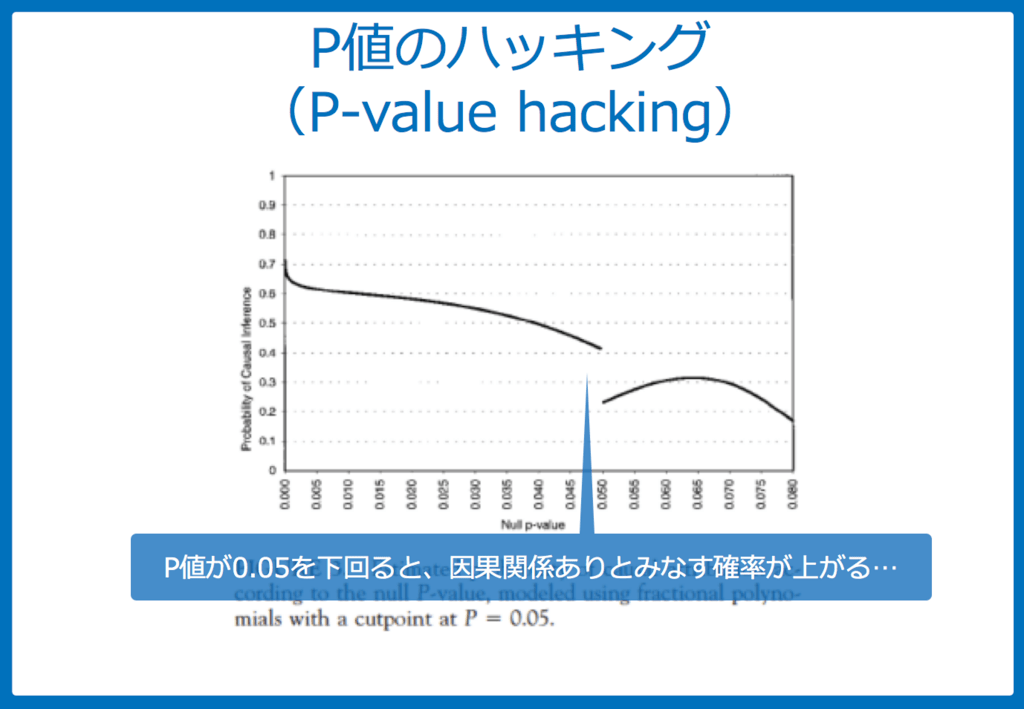
上の図は、Holmanらが行った研究で、研究結果(主にP値)をみて疫学者が「治療効果あり(因果関係あり)」とみなすかみています。
- Y軸が因果関係ありとする確率
- X軸はP値
です。
見ての通り、P値が0.05を切った途端に、「因果関係あり」とみなす確率が増えています。本来は統計のリテラシーのあるはずの疫学者ですらこの結果です。
P値が0.04でも0.06でも、本来は大きな違いはありません。
魔法の数字(P = 0.05)を切った瞬間に大喜びする方(臨床試験をサポートする方や臨床医)を多数みてきましたが(もちろん、その気持ちだけは分かりますが…)、P値が0.05を下回るか否かは、本来は全く重要ではありません。
この現象は雑誌を投稿する側だけでなく、ジャッジする査読者のほうでも起こっています。
「統計学的な有意差のある」研究のほうが、はるかにアクセプトされやすい現象は、どの雑誌でも起こっています。
論文をたくさん投稿している研究者であれば、この現象が理解できると思います。
出版バイアスの評価方法としての Funnel Plot
出版バイアスを評価する方法として、Funnel Plot があります。
Funnel Plotは2つの軸で構成されており、
- X軸:治療効果(Effect estimate)
- Y軸:研究のサイズの指標(多くはStandard error)
をみています。
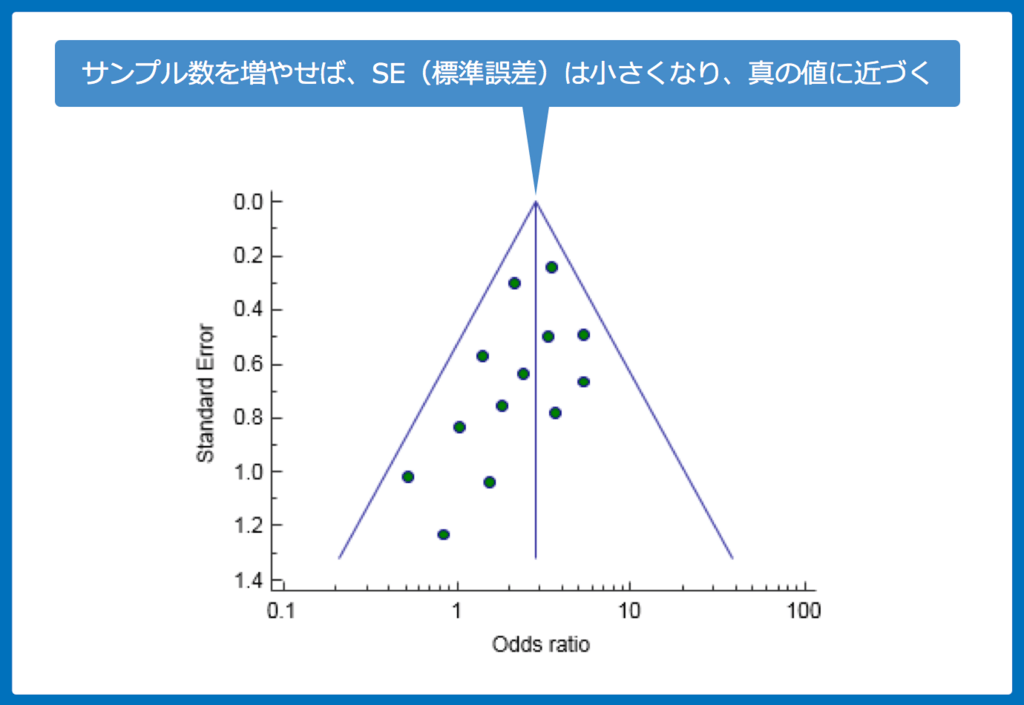
『Funnel』は『漏斗』を意味しますが、ちょうど漏斗を逆さにした形になっているのが分かるでしょう。
通常、サンプル数を多くすれば、標準誤差(Standard Error:SE)は小さくなり、偶然による誤差も小さくなるので、真の値に近づきます。
このため、Funnel Plotをみると、標準誤差(SE)が小さくなるにつれて、治療効果(今回はOR)のばらつきが減り、1箇所に集約された形(まさに逆の漏斗型)になっているのが分かるでしょう。
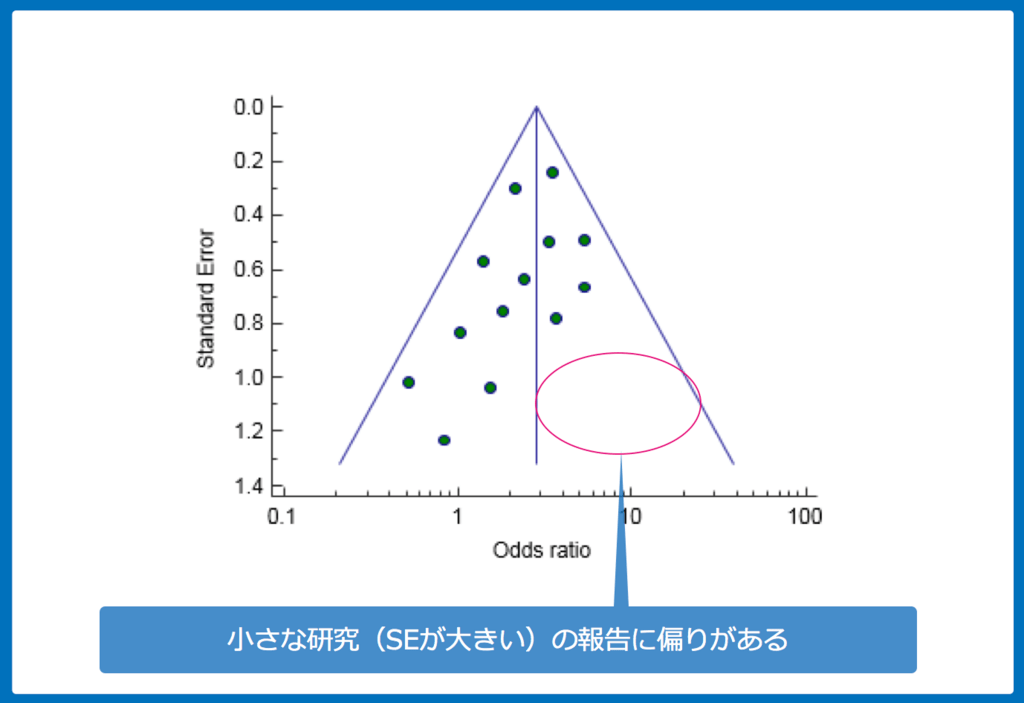
よくみてみると、右下が空白となっています。これは、小さな研究の報告の偏り(つまり出版バイアス)があったことを示唆しています。
このような現象が起こる理由は様々ですが、
- すでに大規模(SEの小さい)研究で同様の結果がある
(今回の例でいうとOR > 3) - 小さな研究では、「すでに報告されているから」という理由でアクセプトされない
- 小さな研究でも「OR < 2」は報告が少ないからアクセプトされる
という現象が重なると、このような形になったのでは、と推察できます。
Funnel Plotが非対称なら必ず出版バイアスか?
このように説明すると
『Funnel Plot で非対称性があるので、これは出版バイアスです』
とステレオタイプに考えたくなります。ですが、あっていることも、間違っていることもあります。
なぜなら、別の理由で同じ現象が起こっていることもあるからです。
例えば、
- 小規模で行われたハイリスクの患者のみで有効だった
- 小規模な研究が先に行われ、(研究された治療以外の)標準治療が確立されたため、後に行われた大規模試験で異なる結果が出た
- 小規模な研究のほうが(参加者が少ない分)、手厚く治療された
などでも同じようなfunnel plotになります。
まとめ
今回は出版バイアスとFunnel Plotについて説明してきました。
Funnel Plotだけでも、相当に奥が深いのがわかっていただけたと思います。
読者の皆様には、ステレオタイプな考え方と、例外があることを理解していただければ十分です。
次回は、出版バイアスの統計学的な検定方法(Egger’s testとBegg’s test)を中心に解説していきます。
おすすめ本はこちら